PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

ĐỀ BÀI

DẠNG 1. Phương trình tích

Câu 1. (SBT-CTST) Giải các phương trình:

a) \(12x\left( {2x - 9} \right) = 0\);

b) \(\left( {1,5t - 4,5} \right)\left( {0,3t + 6} \right) = 0\);

c) \(\left( {\frac{2}{3}x - 4} \right)\left( {\frac{5}{2}x + 3} \right) = 0\)

Câu 2. (SBT-CTST) Giải các phương trình:

a) \(7x\left( {2x - 5} \right) = 0\);

b) \(\left( {3x - 6} \right)\left( {4x + 9} \right) = 0\);

c) \(\left( {\frac{3}{2}x - 2} \right)\left( {\frac{1}{4}x + 3} \right) = 0\)

d) \(\left( {1,5t - 6} \right)\left( {0,3t + 9} \right) = 0\).

DẠNG 2. Phương trình quy về phương trình tích

Câu 3. (SBT-CD) Giải các phương trình:

a) \(\left( {\frac{1}{2}x - \frac{7}{5}} \right)\left( {3x - \frac{5}{8}} \right) = 0\);

b) \(\left( {2x + 3} \right)\left( {x + 1} \right) = \left( {3x + 1} \right)\left( {x + 1} \right)\);

c) \(\frac{1}{4}{x^2} - {(3x - 2)^2} = 0\).

Câu 4. (SBT-CTST) Giải các phương trình:

a) \(5x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0\);

b) \(7x\left( {x + 4} \right) - 3x - 12 = 0\);

c) \({x^2} - 2x - \left( {5x - 10} \right) = 0\);

d) \({(5x - 2)^2} - {(x + 8)^2} = 0\);

Câu 5. (SBT-KNTT) Giải phương trình \({(2x - 1)^2} - 9{x^2} = 0\).

Câu 6. (SBT-KNTT) Giải phương trình \(4{x^2} + {(2x - 3)^2} - 9 = 0\).

Câu 7. (SBT-KNTT) Giải phương trình \({x^2} - 2x = x - 2\).

Câu 8. (SBT-KNTT) Giải các phương trình sau:

a) \({(x + 2)^2} - \left( {2x + 1} \right)\left( {x + 2} \right) = 0\);

b) \(16{x^2} - {(3x + 2)^2} = 0\).

Câu 9. (SBT-KNTT) Giải các phương trình sau:

a) \({x^3} + 3{x^2} - 8 = {x^3} + 2{x^2} - 7\);

b) \(x\left( {2x - 5} \right) = \left( {2x + 1} \right)\left( {5 - 2x} \right)\).

Câu 10. (SBT-KNTT) Giải các phương trình sau:

a) \({x^2} + x = - 6x - 6\);

b) \(2{x^2} - 2x = x - 1\).

DẠNG 3. Tìm điều kiện xác định phương trình chứa ẩn ở mẫu

Câu 11. (SBT-CD) Tìm điều kiện xác định của mỗi phương trình sau:

a) \(\frac{{7x}}{{12 - x}} = 10\);

b) \(\frac{x}{2} - \frac{7}{5} = \frac{x}{{2x - 5}}\);

c) \(\frac{{13}}{{5x + 1}} - 1 = \frac{{8x}}{{x - 3}}\).

Câu 12. (SBT-CD) Tìm điều kiện xác định của mỗi phương trình sau:

a) \(\frac{{13}}{{4 - {x^2}}} = 1\);

b) \(\frac{x}{2} - \frac{1}{5} = \frac{{{x^2}}}{{x - 3}}\);

c) \(\frac{3}{{ - 5x + 5}} - 3x = \frac{{12x}}{{{x^2} - 1}}\).

Câu 13. (SBT-KNTT) Giải các phương trình sau:

a) \(\frac{{5x - 1}}{{3x + 2}} - \frac{{5x + 2}}{{3x}} = 0\);

b) \(\frac{{6x - 5}}{{2x - 1}} - \frac{{9x}}{{3x - 1}} = 0\).

Câu 14. (SBT-KNTT) Giải các phương trình sau:

a) \(\frac{3}{{x + 2}} + \frac{x}{{{x^2} - 2x + 4}} = \frac{{4{x^2}}}{{{x^3} + 8}}\);

b) \(\frac{3}{{2x + 1}} + \frac{7}{{3x + 2}} = \frac{{21x + 10}}{{\left( {2x + 1} \right)\left( {3x + 2} \right)}}\).

DẠNG 4. Giải phương trình chứa ẩn ở mẫu

Câu 15. (SBT-CD) Giải các phương trình:

a) \(\frac{{{x^2}}}{{1 - 2x}} + \frac{{1 + 2x}}{4} = 1\);

b) \(\frac{7}{{x + 4}} - \frac{2}{{x - 7}} = 0\).

Câu 16. (SBT-CD) Giải các phương trình:

a) \(\left( {3x + 5} \right)\left( {\frac{{12}}{5} - 2x} \right) = 0\);

b) \({(7x - 1)^2} = 4{(1 - 2x)^2}\);

c) \(\frac{{2{x^2}}}{{4x + 3}} - \frac{{4x - 3}}{8} = 1\);

\(\left. {{{\rm{d}}^{\rm{*}}}} \right)\frac{x}{{{x^2} + 4x - 5}} - \frac{2}{{x - 1}} = 0\).

Câu 17. (SBT-CTST) Giải các phương trình:

a) \(\frac{{2x + 7}}{{x - 3}} + 1 = \frac{{ - 5}}{{x - 3}}\);

b) \(\frac{{3x + 2}}{{x + 1}} + \frac{8}{x} = 3\);

c) \(\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\)

Câu 18. (SBT-CTST) Giải các phương trình:

a) \(\frac{{2x + 5}}{{x - 3}} + 1 = \frac{5}{{x - 3}}\)

b) \(\frac{{5x + 2}}{{x + 1}} + \frac{3}{x} = 5\);

c) \(\frac{{x + 1}}{{x - 3}} + \frac{{x + 3}}{{x - 1}} = 2\);

d) \(\frac{{x + 4}}{{x - 4}} - \frac{{x - 4}}{{x + 4}} = \frac{{64}}{{{x^2} - 16}}\)

Câu 19. (SBT-KNTT) Giải phương trình \(\frac{{3x}}{{2x + 3}} - \frac{{6x}}{{4x - 1}} = 0\).

Câu 20. (SBT-KNTT) Giải phương trình \(\frac{1}{{2x - 1}} + \frac{3}{{2x + 1}} = \frac{{6x - 3}}{{4{x^2} - 1}}\).

DẠNG 5. Bài toán thực tế-hình học phẳng

Câu 21. (SBT-CD) Một khu đất có dạng hình chữ nhật với chiều dài hơn chiều rộng \(16{\rm{\;m}}\). Trên khu đất đó, người ta làm một mảnh vườn trồng hoa có dạng hình thoi \(ABCD\) với đường chéo \(AC\) bằng chiều rộng của khu đất và đường chéo \(BD\) bằng chiều dài của khu đất (Hình 1). Tính chiều dài của khu đất,

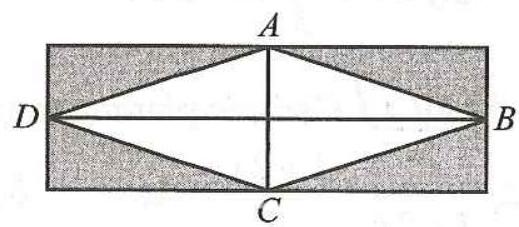
Hinh 1 biết diện tích của phần đất còn lại là \(96{\rm{\;}}{{\rm{m}}^2}\).

Câu 22. (SBT-CD) Một mảnh vườn có dạng hình chữ nhật với chiều rộng là \(10{\rm{\;m}}\). Chủ vườn đã làm con đường thảm cỏ (phần tô màu xám) với các kích thước như Hinh 2.

a) Tính chiều dài của mảnh vườn, biết tỉ số giữa diện tích của con đường thảm cỏ và diện tích của mảnh vườn là \(\frac{1}{3}\).

b) Biết rằng chi phí để hoàn thành mỗi mét vuông của con đường thảm cỏ là 100000 đồng. Tính số tiền mà chủ vườn đã chi để làm con đường thảm cỏ đó.

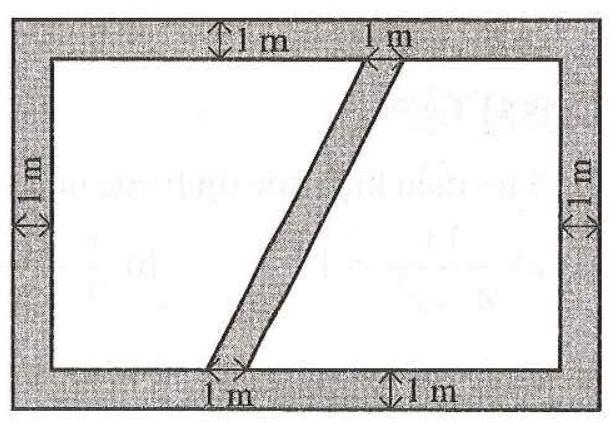
Hinh 2

DẠNG 6. Bài toán thực tế-năng suất dự kiến, thực tế

Câu 23. (SBT-CD) Một công nhân dự định làm 14 sản phẩm trong thời gian đã định. Nhưng trên thực tế công ty đã giao 21 sản phẩm nên để hoàn thành đúng thời gian đã định, người đó phải làm mỗi giờ thêm 3 sản phẩm. Tính năng suất dự định của công nhân đó.

Câu 24. (SBT-CTST) Một nhóm thợ đóng giày dự định hoàn thành kế hoạch trong 26 ngày. Nhưng do cải tiến kĩ thuật nên mỗi ngày đã vượt mức 6 đôii giày, do đó chẳng những nhóm thợ đã hoàn thành kế hoạch đã định trong 24 ngày mà còn vượt mức 104 đôi giày. Tính số đôi giày nhóm thợ phải làm theo kế hoạch.

DẠNG 7. Bài toán thực tế-chuyển động

Câu 25. (SBT-CD) Một ô tô đi quãng đường \(AB\) dài \(61,5{\rm{\;km}}\). Sau khi đi được \(30{\rm{\;km}}\) với tốc độ không đổi, ô tô đi tiếp quãng đường còn lại với tốc độ tăng thêm \(2{\rm{\;km}}/{\rm{h}}\). Tính tốc độ ban đầu của ô tô, biết thời gian ô tô đi trên \(30{\rm{\;km}}\) đầu bằng thời gian ô tô đi trên \(31,5{\rm{\;km}}\) còn lại.

Câu 26. (SBT-CD) Một ca nô đi xuôi đòng từ địa điểm \(A\) đến địa điểm \(B\), rồi lại đi ngược dòng từ địa điểm \(B\) trở về địa điểm \(A\). Thời gian ca nô đi xuôi dòng và thời gian ca nô đi ngược dòng chênh lệch nhau 40 phút. Tính tốc độ của ca nô khi nước yên lặng. Biết rằng độ dài quãng đường \(AB\) là \(24{\rm{\;km}}\), tốc độ của dòng nước là \(3{\rm{\;km}}/{\rm{h}}\) và tốc độ của ca nô khi nước yên lặng không đổi trên suốt quãng đường.

Câu 27. (SBT-CTST) Một người đi xe đạp từ A đến B cách nhau 60 km. Sau đó 1 giờ, trên cùng quãng đường đó, một xe máy cũng đi từ A đến B và đến B sớm hơn xe đạp 2 giờ. Tính tốc độ của mỗi xe, biết rằng tốc độ của xe máy gấp 4 lần tốc độ của xe đạp.

Câu 28. (SBT-CTST) Một người dự định đi bằng ô tô trên quãng đường AB dài 120 km trong một thời gian nhất định. Nửa quãng đường đầu xe đi vào đường cao tốc với tốc độ hơn dự định \(15{\rm{\;}}km/h\). Sau khi ra khỏi đường cao tốc, trên nửa quãng đường còn lại, xe đi với tốc độ chậm hơn dự định \(10{\rm{\;}}km/h\). Biết ô tô đến đúng giờ đự định. Tính thời gian dự định đi quãng đường AB của người đó.

DẠNG 8. Bài toán thực tế-tìm số

Câu 29. (SBT-CD) Cho một phân số có mẫu số lớn hơn tử số là 2. Nếu bớt tử số đi 3 đơn vị và bớt mẫu số đi 6 đơn vị thì ta được một phân số mơi bằng phân số nghịch đảo của phân số đã cho. Tìm phân số đó.

Câu 30. (SBT-CTST) Một phân số có tử số bé hơn mẫu số 9 đơn vị. Nếu thêm tử số 1 đơn vị và thêm mẫu số 2 đơn vị thì được phân số mới bằng \(\frac{1}{3}\). Tìm phân số đã cho.

DẠNG 9. Bài toán thực tế-vật lí

Câu 31. (SBT-CD) Biết khối lượng riêng của kim loại \({\rm{A}}\) lớn hơn khối lượng riêng của kim loại \({\rm{B}}\) là \(6,24{\rm{\;kg}}/{{\rm{m}}^3}\). Thể tích của \(45{\rm{\;kg}}\) kim loại \({\rm{B}}\) bằng thể tích của \(149{\rm{\;kg}}\) kim loại \({\rm{A}}\). Tính khối lượng riêng của kim loại \({\rm{B}}\).

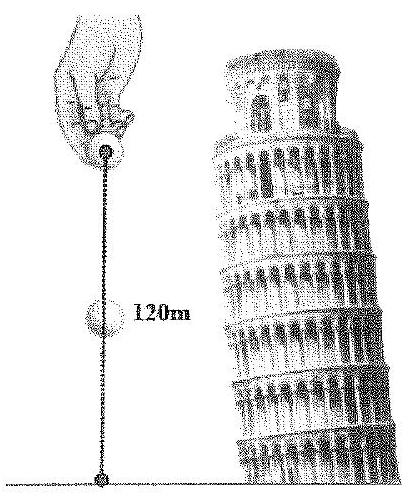
Câu 32. (SBT-KNTT) Một vật rơi tự do từ độ cao so với mặt đất là 120 mét. Bỏ qua sức cản không khi, quãng đường chuyển động \(s\) (mét) của vật rơi tự do sau thời gian \(t\) được biểu diễn gần đúng bởi công thức \(s = 4,9{t^2}\), trong đó \(t\) là thời gian tính bằng giây. Sau bao nhiêu giây kể từ khi bắt đầu rơi thì vật này chạm mặt đất (làm tròn kết quả đến chữ số hàng đơn vị)?

DẠNG 10. Bài toán thực tế-tính tiền

Câu 33. (SBT-CD) Bác Lan dự định dùng hết số tiền 480 nghìn đồng để mua gạo nếp gói bánh chưng nhân dịp tết Nguyên đán. Khi đến cửa hàng, loại gạo mà bác Lan dự định mua đã tăng 2 nghìn đồng \(/{\rm{kg}}\). Do vậy, bác Lan đã mua lượng gạo giảm \(\frac{1}{{16}}\) lần so với dự định. Tính giá tiền mỗi kilôgam gạo mà bác Lan đã mua.

DẠNG 11. Bài toán thực tế-vòi nước

Câu 34. (SBT-CTST) Một vòi nước chảy vào một bể không có nước. Cùng lúc đó một vòi khác chảy từ bể ra mỗi giờ lượng nước chảy ra bằng \(\frac{4}{5}\) lượng nước chảy vào. Sau 5 giờ nước trong bể đạt \(\frac{1}{8}\) dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu đầy bể?